 2023-2024学年北师大版必修第一册 正弦函数余弦函数的图象与性质 作业.docx
2023-2024学年北师大版必修第一册 正弦函数余弦函数的图象与性质 作业.docx
《2023-2024学年北师大版必修第一册 正弦函数余弦函数的图象与性质 作业.docx》由会员分享,可在线阅读,更多相关《2023-2024学年北师大版必修第一册 正弦函数余弦函数的图象与性质 作业.docx(4页珍藏版)》请在第一文库网上搜索。
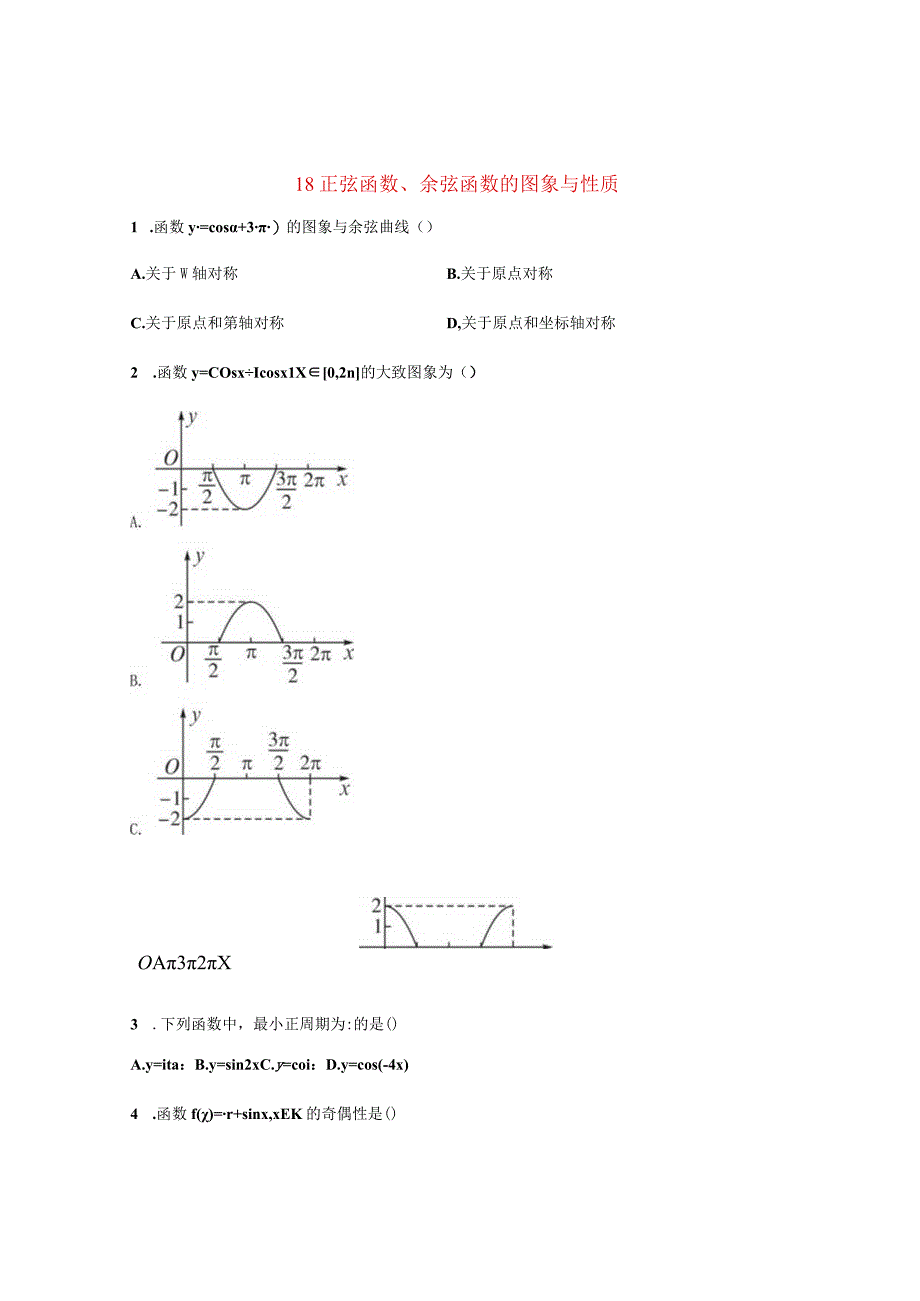
1、18正弦函数、余弦函数的图象与性质1 .函数y=cos+3)的图象与余弦曲线()A.关于W轴对称B.关于原点对称C.关于原点和第轴对称D,关于原点和坐标轴对称2 .函数y=COsxIcosx1X0,2n的大致图象为()OA32X3 .下列函数中,最小正周期为:的是()A.y=ita:B.y=sin2xC.y=coi:D.y=cos(-4x)4 .函数f()=r+sinx,xEK的奇偶性是()A.奇函数B.偶函数C.既是奇函数又是偶函数D.既不是奇函数,也不是偶函数5 .函数y=-8SX在区间一;,B上()A.单调递增B.单调递减C.先减后增D.先增后减6 .函数y=2Sinx的最大值及取最大值
2、时X的值为()A.3,X=JB.1,x=+2k(JcZ)C.3,x=-+2kZ1).3,x=+2k(Z)227 .(多选题)正弦函数y=SjnX,K的图象的一条对称轴是(BC).y轴B.直线X=-C.直线X=-D.直线JC=8 .函数y=X:-CQSX的零点个数为.9 .已知函数f()是定义在R上的周期为6的奇函数,且f(1)=1,则f(5)二10 .已知函数*)=由(5+:)(.0)的最小正周期为TT,则(一;)=.11 .函数y=328s(m+:)的最大值为,此时X=.12 .函数y=cos(z+E)xW0彳的值域为.13 .用“五点法”作出函数V=1+2sinx,0,2可的简图.14 .
3、求函数y=;sin(m-x),W0w的单调递增区间.18正弦函数、余弦函数的图象与性质1. C解析因为y=COSG+3TT)=-CoSX所以其图象与余弦函数V=CoM的图象关于原点和*轴都对称.2. D解析由题意得w.32cosrv04x4或2贡4”4讥3. D4. A解析由/(r)=-X+sin(-x)=-x-sinx=-f(x)可知/(x)是奇函数.5. C解析结合函数在区间一;,手上的图象可知C正确.6. C解析因为Si11X-1J,所以当=-1,即X=-g+2kn=x4y=8=的图象,如图所示.由图可知两个函数图象有两个交点,故函数y=2-CoSX的零点个数为2.解析=f(5-6)=/(T)=-r=-110.-2解析,f(x)的最小正周期为,,0,=,上=Z.“*)=而Qx+;,./(_:)=sin(-2xg+=疝=-Sin;=-jH.52fc(Z)解析函数y=3-2cos(x胃的最大值为5,此时X+:=H+2kn(kZ),即X=Z1(fcZ)12 -?解析:0X-,X+261632n,/,:.COSCOS+-Jcos-,-Jy,即函数的值域为卜:,斗13 .解列表:K0U232nSiI1X010-101+2SinX131-11描点、连线,如图所示.令三十2kX-:S兰十2tfcZ即g2WiXsy2v,*WZXxPV1所以FX,所以该函数的单调递增区间为三,a


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2023-2024学年北师大版必修第一册 正弦函数余弦函数的图象与性质 作业 2023 2024 学年 北师大 必修 一册 正弦 函数 余弦 图象 性质
 第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 调和油系列产品项目可行性研究报告.doc
调和油系列产品项目可行性研究报告.doc

