 第四章矩阵分解改.docx
第四章矩阵分解改.docx
《第四章矩阵分解改.docx》由会员分享,可在线阅读,更多相关《第四章矩阵分解改.docx(49页珍藏版)》请在第一文库网上搜索。
1、第四章矩阵分解基于理论研究和计算的需要,往往有必要把矩阵分解为具有某种特性的矩阵之和或积,这就是我们所说的矩阵分解.本章将介绍一些常用的分解方法,某些在计算方法中已涉及的分解,我们这里就不再提起了.4.1矩阵的正交三角分解60年代后以Givens与Househo1den变换发展起来的矩阵的QR分解在计算数学中扮演了十分重要的角色,尤其是以QR分解所建立的QR方法,已对数值线性代数理论的近代发展起了关键作用.定义1如果一个上三角矩阵的主对角线元素全为正实数,则称该矩阵为一个正线上三角矩阵.定理1(正交三角分解)设A为阶实满秩矩阵,则必有阶正交矩阵。及阶正线上三角矩阵R,使得A=QR.证设A按列分
2、块为A=(1,2,),则囚,见,,%为欧氏空间R”的一组基,利用施密特正交化方法可以得到一组正交基-a=一岩Si+%+,A=1XnaX+,2+-1-1+an再单位化得一组标准正交基=如4,2=bv2a1+b22a2,(1)”=but%+b2na2+,n-+bnnan其中,=占0,令b.hu2unB=显然B为正线上三角矩阵.且有b22hIn,bnn,(巧,知,“)=(,%,,%)B(2)再令Q=,火,与),则Q为正交矩阵.记R=B1则R仍为正线上三角矩阵.由(2)即得A=QR.定理证毕.实满秩矩阵的QR分解是唯一的.例1求矩阵22、A=212J2的QR分解解记A的三个列向量依次为用施密特正交化方
3、法得令。=(,”3)其中B1e-1313,16oO经计算得R=8-=*立3也263o76。,便有A=QR2=-x+a2=(1,T1),1711A=-A-A3=(*-)3622单位化得8嗑=%=塌熹金2=a=,+2=f,i=ii=-j2a1-a2+T2,=(-,0,-y-)r.2O,则。为正交矩阵.且2一名4-洌3612国T.O2对于复满秩矩阵,类似地有UR分解定理。定理2设4为拉阶复满秩矩阵,则必有阶酉矩阵U及正线上三角矩阵R,使得4=UR以下讨论列满秩矩阵的正交三角分解定理3设An”为实数域上的列满秩矩阵,则有分解式A=QR9R=o,其中。为机阶正交矩阵,R1为阶正线上三角矩阵.证不防设机,
4、由4列满秩,必可找到相(m-)的列满秩矩阵A”使人=(AA)为历阶满秩矩阵,由定理1必有机阶正交矩阵。及,阶正线上三角矩阵A,使得A=QR.记A的前列形成的矩阵为R=(K,则与为阶正线上三角矩阵.且显然有A=QR.对于复数域上的列满秩矩阵,亦有类似结果.定理4设AE为复数域上的列满秩矩阵,则有A=UR,R=(R1,(3)j其中U为加阶酉矩阵,与为阶正线上三角矩阵.设m,如记,U=(3h,GU=(5),U1(K2,,),因为是酉矩阵U的前列构成的,通常称之为部分酉阵,它满足qq=g.从(3)式可见(4)(3)式与(4)式都可以看作是列满秩矩阵的UR分解.4.2矩阵的满秩分解下面介绍矩阵的满秩分解
5、.定理5(满秩分解)对任一秩为r(rO)的矩阵必存在秩为r的矩阵纥Xr及Gw使得A=BC.(1)证4可经初等变换化为标准形,即有机阶满秩矩阵4及阶满秩矩阵巴,使得小o)(E(E于是A=7W=中;(4,。)-uk7令54,0)星,则6是Pj的前歹J,C是尸2”的前r行,当然有秩8二秩C=r,并使A=BC,定理证毕.满秩分解(1)通常不是唯一的.它取决于行列的初等变换矩阵6及鸟.而矩阵6、鸟可以在化A为标准形的过程中顺便得到,具体做法是:对如下矩阵AEj也O)的前加行、前列施行一系列初等变换,化4为标准形.在这一过程中,等于对纥(及线)分别施以了与A的变化相同的行的(及列的)初等变换.最终化为B与
6、C.例1求矩阵2O0、A=271-3JTT3,的一种满秩分解.解在用行、列初等变换化A为标准形式过程中,顺便求出相应的初等变换矩阵丹,月,具体变换过程如下:(AE200271-31-1-13100、010001-2r+r2-r+、1200031-30-3-13100、-210-101100001000010,0001100001000010.0001U。厂/e+G-2c1+c2rI000031-30000100、-210-3116cq1000013-30000100、-210-3111-20001000010poo1/10-2000100100,0001Zp00010OA0100-210000

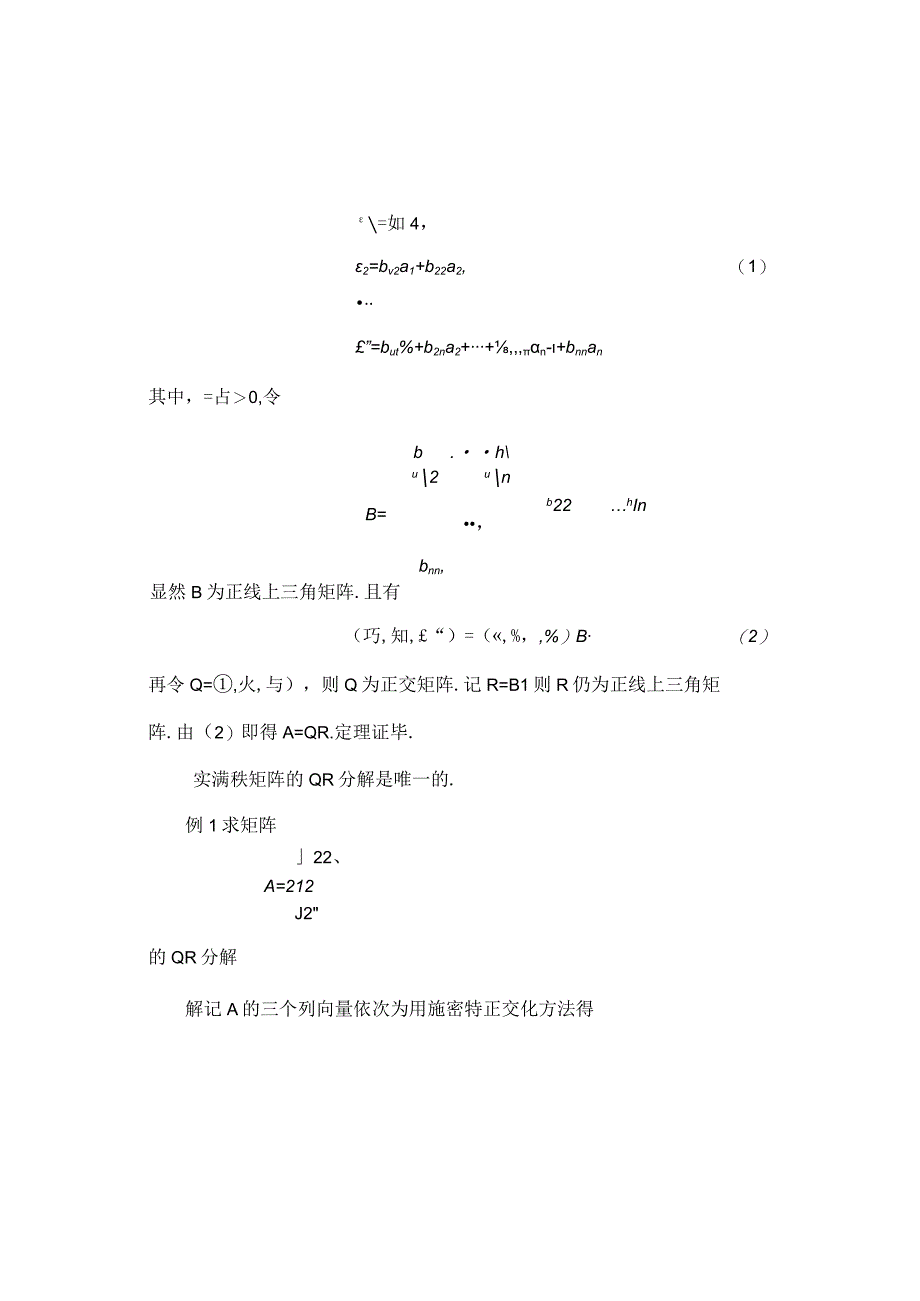

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 第四 矩阵 分解
 第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 调和油系列产品项目可行性研究报告.doc
调和油系列产品项目可行性研究报告.doc

