 三角函数2公开课教案教学设计课件资料.docx
三角函数2公开课教案教学设计课件资料.docx
《三角函数2公开课教案教学设计课件资料.docx》由会员分享,可在线阅读,更多相关《三角函数2公开课教案教学设计课件资料.docx(15页珍藏版)》请在第一文库网上搜索。
1、三角函数专题21 .如图1为某智能洗拖一体扫地机,它正常工作及待机充电时的示意图如图2所示,四边形ABCD为它的手柄,OE为支撑杆,OM为拖把支架,且点O始终在AB的延长线上,当待机时,BC/OM,已知AB=I8。,BC=I5cm,ZABC=ZC=90o,AD+CD=21cm,则8=cm;OE绕点O逆时针旋转一定角度,机器开始工作,当,C,M在同一直线上时,点A,B分别绕。点旋转到点A,B,且高度分别下降了21.6Cm和18cm,则此时点。到OM距离为cm.2 .图1是可折叠琴谱架上半部分的实物图,图2是图1的平面示意图(琴谱架钢条的宽度忽略不计),四边形ACZ)/为矩形,AC=1AF=32c
2、m,B、E分别为AC、。尸的中点,H、2G分别为AR。的中点.MN,PQ为滑动轨道,滑道MN比小4cm,折叠琴谱架时,A”上点X、尸”上点Y分别在滑道MMPQ上滑动时,各钢条可以绕连接点A、B、C、D、E、F、G、H、0转动.当点X、Y分别滑到N、。时,此时A、8、C、。、E、F、G、H、O、M、N、P、Q、X、Y在一条直线上.(1)琴谱架中ON的长为cm.3 (2)当琴谱架折叠成图3,图4是图3的平面示意图,当氏H、E三点共线时,求滑动4 .图1是一折叠桌,桌板OE固定墙上,支架AD,HE绕同D,七旋转时,AD/HE,桌板边缘A”BG。尸/)E,桌脚AN_1A”,桌子放平得图2.图3是打开过
3、程中侧面视图,当点N在直线C尸上时,点N到墙OE的距离为cm.视图中以C,K为顶点的长方形表示一圆柱体花瓶,桌子打开至点M,C,尸在同一直线时,桌板边缘G1恰卡在点K,为不影响桌板BG收放,则至少将花瓶沿b方向平移所.5 .如图1是个家用折叠梯子,使用时四个踏板都是平行于地面且全等的矩形,BC=CD=DE=E1,将踏板往上收起时(如图2),点A与点尸重合,此时,踏板可以看作与支架A1重合,将梯子垂直摆放时,量得点A离地面I1Ocm,点H离地面65cm,则踏板宽8F=cm;图3是图1的简略视图,记支架AM交BF于点P,此时点G恰好在A的正下方,且量得P8:PF=I3:4,则AM=cm.6 .如图
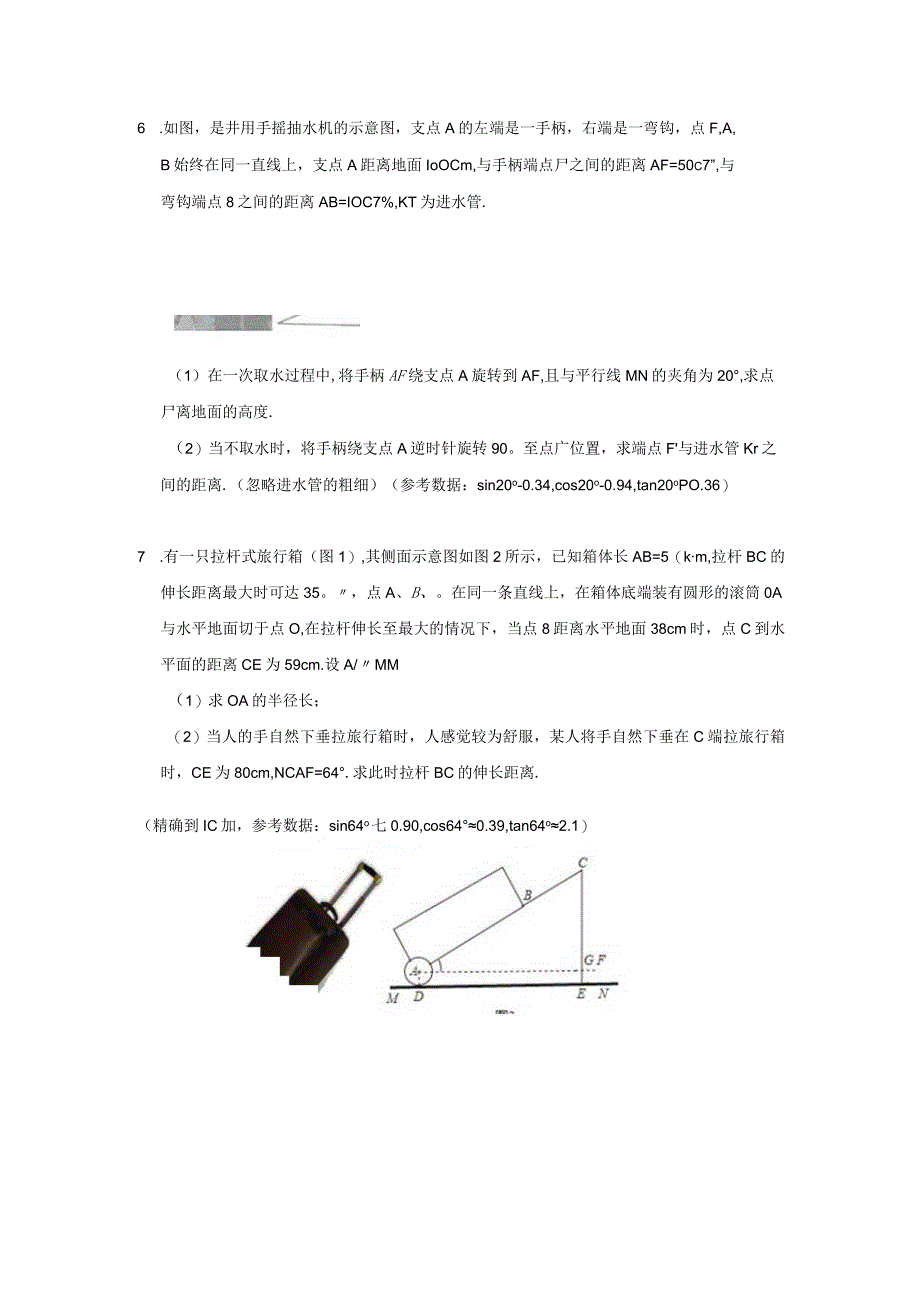
4、,是井用手摇抽水机的示意图,支点A的左端是一手柄,右端是一弯钩,点F,A,B始终在同一直线上,支点A距离地面IoOCm,与手柄端点尸之间的距离AF=50c7”,与弯钩端点8之间的距离AB=IOC7%,KT为进水管.(1)在一次取水过程中,将手柄AF绕支点A旋转到AF,且与平行线MN的夹角为20,求点尸离地面的高度.(2)当不取水时,将手柄绕支点A逆时针旋转90。至点广位置,求端点F与进水管Kr之间的距离.(忽略进水管的粗细)(参考数据:sin20o-0.34,cos20o-0.94,tan20oPO.36)7 .有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=5(km,拉杆
5、BC的伸长距离最大时可达35。,点A、B、。在同一条直线上,在箱体底端装有圆形的滚筒0A与水平地面切于点O,在拉杆伸长至最大的情况下,当点8距离水平地面38cm时,点C到水平面的距离CE为59cm.设A/MM(1)求OA的半径长;(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为80cm,NCAF=64.求此时拉杆BC的伸长距离.(精确到IC加,参考数据:sin64o七0.90,cos640.39,tan64o2.1)8 .为营造“安全出行”的良好交通氛围,实时监控道路交通,某市交管部门在路口安装的高清摄像头如图所示,立杆MA与地面48垂直,斜拉杆C。与
6、AM交于点C,横杆OE/AB,摄像头打_1OE于点EAC=5.5米,CO=3米,E尸=0.4米,NCDE=I62.AB(1)求NMCD的度数;(2)求摄像头下端点尸到地面AB的距离.(精确到百分位)(参考数据;sin72o=0.95,cos72o0.31,tan72o=3.08,sin18七0.31,cos18o0.95,tan!8oy0.32)9 .某挖掘机的底座高AB=O.8米,动臂BC=1.2米,Co=I.5米,BC与CZ)的固定夹角NBCD=I40;初始位置如图1,斗杆顶点。与铲斗顶点E所在直线OE垂直地面AM于点E测得NCz)E=70(示意图2).工作时如图3,动臂BC会绕点B转动,
7、当点A,B,C在同一直线时,斗杆顶点。升至最高点(示意图4).(1)求挖掘机在初始位置时动臂BC与AB的夹角ZABC的度数.(2)问斗杆顶点。的最高点比初始位置高了多少米?(精确到0.1米)(参考数据:sin50o-0.77,cos50oQO.64,sin70o0.94,cos70oAo.34,3555=j1.73)10 .如图1是某路灯,图2是此路灯在铅垂面内的示意图,灯芯A在地面上的照射区域BC长为7米,从8,C两处测得灯芯A的仰角分别为和,且tan=6,tan0=1.(1)求灯芯A到地面的高度.(2)立柱。E的高为6米,灯杆。尸与立柱OE的夹角No=I20,灯芯A到顶部尸的距离为1米,且


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 三角函数 公开 教案 教学 设计 课件 资料
 第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 调和油系列产品项目可行性研究报告.doc
调和油系列产品项目可行性研究报告.doc

