 成考专升本高数第四章笔记.docx
成考专升本高数第四章笔记.docx
《成考专升本高数第四章笔记.docx》由会员分享,可在线阅读,更多相关《成考专升本高数第四章笔记.docx(6页珍藏版)》请在第一文库网上搜索。
1、第四章多元函数微积分初步4.1偏导数与全微分.主要内容:.多元函数的概念1 .二元函数的定义:z=f(x9y)(x,j)D定义域:/)(/)2 .二元函数的几何意义:二元函数是一个空间曲面。(而一元函数是平面上的曲线).二元函数的极限和连续:1. 极限定义:设z=f(x,y)满足条件:1。在点*0,盟)的某个领域内有定S(点,J)可除外:2o1im(x,j)=AXXoJJo则称=/(x,y)在(乙,盟)极限存在,且等青。2. 连续定义:设z=f(x,y)满足条件:1。在点*0,盟)的某个领域内有定S2o1im(x,j)=/(x0,j0)xJJo则松=/(%,y)在(乙,盟)处连续,。.偏导数:
2、定义:/(巧),在(乙,/)点/;(/,/)/(XO,/)分别为函教(。)在(Xo,/)处对r,y的偏导数。z=(x,y)在。内任意点x,y)处的偏导数记为加,M竽喑*.全微分:1定义:z=f(x,y)若AZ=(x+x,j+y)-/(x,y)=Ax+BAy+o(夕)其中,A、8与Ax、Ay无关,o(p)是比p=J2+4/较高阶的无穷小量。贝!1:dz=df(x,j)=Ax+BSyz=(x,j)在点(x,y)处的全微分。3.全微分与偏导数的关系定理:窃(x,y),W(x,y)连续(X,y)Z贝!:Z=/(x,y)在点x,y)处可微且dz=fc(x9y)dx+fy(x,y)dy.复全函数的偏导数:
3、1设:z=f(u,v),u=u(x,y),v=v(x,y)z=m(x,j),v(x,j)r1zuzv贝h+xuxvxzuzvIyuyvy2,设y=/(/),=(X)/=WX)y=小(X)#(%)dyyduydvdxudxvdx伏).隐含数的偏导数:1设小X,z)=O,Z=/(x,y),且理0贝!|包=一段包=_及5xF,JyF;啊X,y)=O,y=/(x),f;O则”三axFy(3二阶偏导数:/、2zGQz%(%)=WT=瓦(工)OXOXOX2zzyoyoy、a,fy(xJ)=羡(三)oxoyyox(、表z了(占了)=工-)yxxy结论:当*(x,y)和(x,y)为x,y的连续函数时则:fK%,y)=f;X(My)(A).二元函数的无条件极值1.二元函数极值定义:设Z(X,y)在(X。,盟)某一个邻域内有定3若Z(X,y)1当xO,y=O0,z(x,0)=-x2+11,驻点不一定是极值点。3 .极值的充分条件:设:函麴=(,y)在(乙,%)的某个领域日有二阶偏导数,目。,盟)为驻点:若:p=A(,/)F-/二(XO,盟),舞(Jo)当:p0且/二(%0,/)耐,=/(%,To)为极小值当:p0,=/(X。,盟)不是极值当:p=0,n不能确定,求二元极值的方法:10求一阶偏导数,令两个阶偏导数等于容解出驻点2。求t,根据极值的充分条件判断驻点是否极值点。3。若驻点是极值点,求极值C


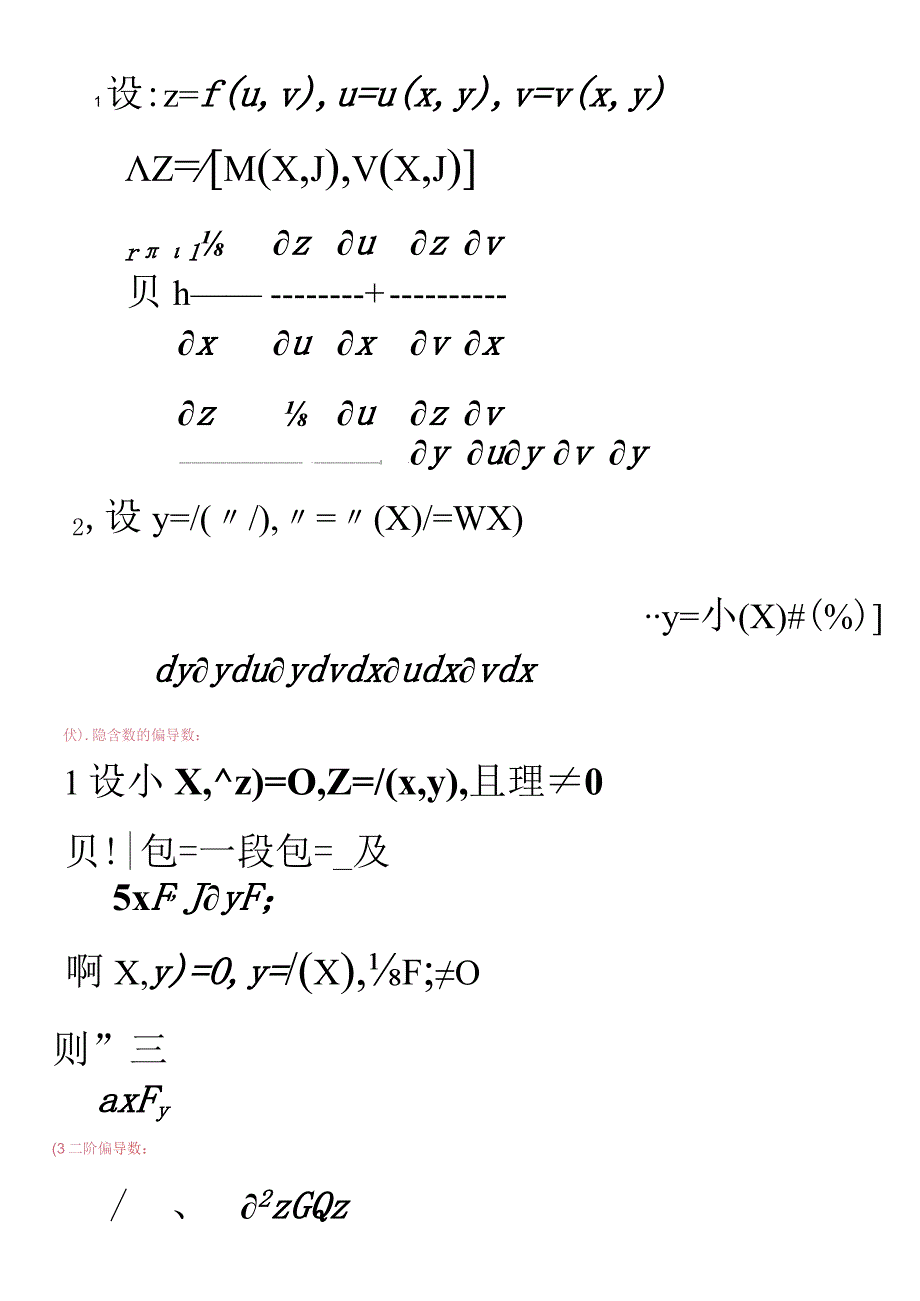
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 成考专升 第四 笔记
 第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 调和油系列产品项目可行性研究报告.doc
调和油系列产品项目可行性研究报告.doc

