 专题29数列知识梳理文原卷版.docx
专题29数列知识梳理文原卷版.docx
《专题29数列知识梳理文原卷版.docx》由会员分享,可在线阅读,更多相关《专题29数列知识梳理文原卷版.docx(7页珍藏版)》请在第一文库网上搜索。
1、专题29数列(知识梳理)一、数列的概念1、数列的定义:按一定次序排列的一列数叫做数列。数列中的每个数都叫这个数列的项。数列的一般形式:1,,或简记为他“O其中可是数列的第1项(又称首项),4是数列的第项(又称通项)。2、通项公式的定义:如果数列4的第项与之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式。3、数列的特性:(对比集合的特性)数列是特殊的数集、点集。(1)有序性:数列的数是按一定次序排列的,因此,如果组成两个数列的数相同而排列次序不同,那么它们就是不同的数列。(2)可异性:定义中并没有规定数列中的数必须不同,因此,同一个数在数列中可以重复出现,如常数列。(3)从函数角
2、度看数列:数列可以看作是一个定义域为正整数集N+(或它的有限子集1,2,3,,)的函数。4、数列的分类:(1)根据数列项数的多少分:有穷数列:项数有限的数列;例如数列1,2,3,4,5,6。是有穷数列。无穷数列:项数无限的数列;例如数列1,2,3,4,5,6是无穷数列。(2)根据数列项的大小分:递增数列:从第2项起,每一项都大于它的前一项的数列。递减数列:从第2项起,每一项都小于它的前一项的数列。常数数列:各项相等的数列。摆动数列:从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列。(3)根据任何一项的绝对值是否小于某一正数可分为:有界数列;无界数列。二、数列的表示方法1、列表法(又
3、称列举法)。2、图像法:图像过一四象限或X轴正半轴,横坐标为正整数。是一系列孤立的点,不像我们前面所研究过的初等函数般都是连续的曲线,因此在解决问题时,要充分利用这一特殊性。3、解析法:用数列的通项公式也就是相应函数的解析式来表示数列。三、根据数列的前项写出这个数列的通项公式1、编号:把序号1、2、3标在相应项上,便于突出第项为与项数的关系,即如何用表示。2、变形:出现正负间隔用(-1)或(T严进行调整。(2)出现分数首先考虑分子、分母是否存在规律,然后考虑通分成同分母分数。(3)找不到规律可以考虑1后再观察。(4)当一个数列间隔几项才具有相同规律(特别是奇数项与偶数项)时,不妨用分段函数来表
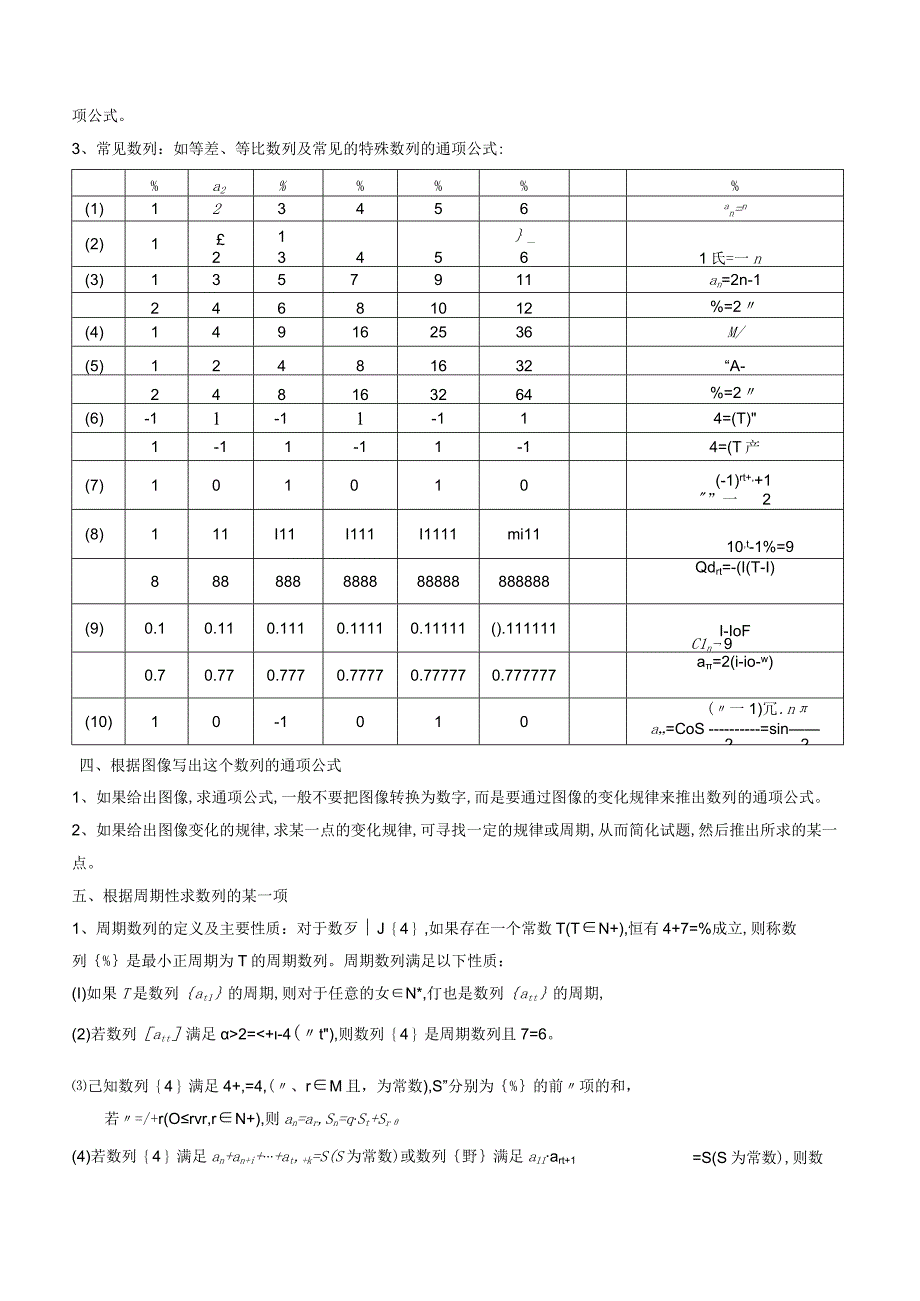
4、示其通项公式。3、常见数列:如等差、等比数列及常见的特殊数列的通项公式:%a2%(1)123456an=n(2)121345_61氏=一n(3)1357911an=2n-124681012%=2(4)149162536M/(5)12481632“A-248163264%=2(6)-11-11-114=(T)1-11-11-14=(T产(7)101010(-1)rt+,+1”一2(8)111I11I111I1111mi1110,t-1%=9888888888888888888888Qdrt=-(I(T-I)(9)0.10.110.1110.11110.11111().111111I-IoFC1n
5、-,90.70.770.7770.77770.777770.777777a=2(i-io-w)(10)10-1010(一1)冗.na=CoS=sin22四、根据图像写出这个数列的通项公式1、如果给出图像,求通项公式,一般不要把图像转换为数字,而是要通过图像的变化规律来推出数列的通项公式。2、如果给出图像变化的规律,求某一点的变化规律,可寻找一定的规律或周期,从而简化试题,然后推出所求的某一点。五、根据周期性求数列的某一项1、周期数列的定义及主要性质:对于数歹J4,如果存在一个常数T(TN+),恒有4+7=%成立,则称数列%是最小正周期为T的周期数列。周期数列满足以下性质:(I)如果T是数列at


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 专题 29 数列 知识 梳理 文原卷版
 第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 调和油系列产品项目可行性研究报告.doc
调和油系列产品项目可行性研究报告.doc

