 诱导公式一 正弦余弦和正切的诱导公式 教学设计.docx
诱导公式一 正弦余弦和正切的诱导公式 教学设计.docx
《诱导公式一 正弦余弦和正切的诱导公式 教学设计.docx》由会员分享,可在线阅读,更多相关《诱导公式一 正弦余弦和正切的诱导公式 教学设计.docx(6页珍藏版)》请在第一文库网上搜索。
1、1.2.4诱导公式(一)一、教学目标1 .通过本节内容的教学,使学生掌握+2br,角的正弦、余弦和正切的诱导公式及其探求思路,并能正确地运用这些公式进行任意角的正弦、余弦和正切值的求解、简单三角函数式的化简与三角恒等式的证明。2 .通过公式的应用,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力。二、教学重点、难点重点:四组诱导公式及这四组诱导公式的综合运用。难点:公式(四)的推导和对称变换思想在学生学习过程中的渗透。三、教学方法先由学生自学,然后由教师设置一些问题供学生思考,在此基础上,可以通过讲授再现概念,通过练习理解概念,完成教学.四、教学过程教学环节教学内容
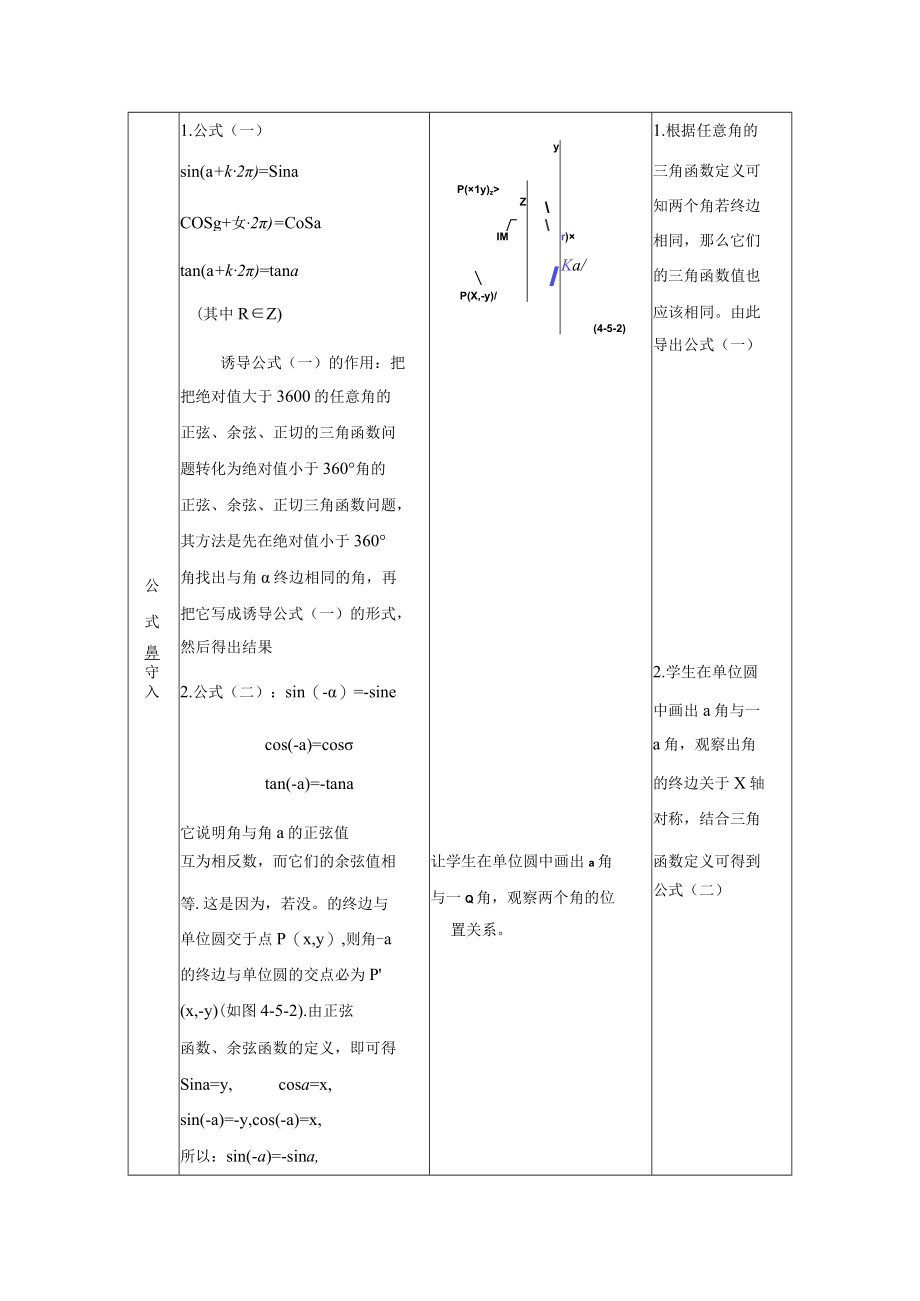
2、师生互动设计意图复习引入1、初中我们已经会求锐角的三角函数值。2、和30、45、60终边相同的角如何表示?本节我们将研究任意角三角函数值之间的某中关系,以及如何求任意角的三角函数值。教师提问:0、30、45、60、90的正弦、余弦、正切的三角函数值是多少?学生回答我们如何求360。、390、-315的三角函数值呢?温故知新1.公式(一)1.根据任意角的ysin(a+k2)=Sina三角函数定义可P(1y)zZ知两个角若终边COSg+女2)=CoSaIMr)相同,那么它们tan(a+k2)=tana/Ka/的三角函数值也P(X,-y)/(其中RZ)(4-5-2)应该相同。由此导出公式(一)诱导公
3、式(一)的作用:把把绝对值大于3600的任意角的正弦、余弦、正切的三角函数问题转化为绝对值小于360角的正弦、余弦、正切三角函数问题,其方法是先在绝对值小于360公角找出与角终边相同的角,再式把它写成诱导公式(一)的形式,鼻然后得出结果守2.学生在单位圆入2.公式(二):sin(-)=-sine中画出a角与一cos(-a)=cosa角,观察出角tan(-a)=-tana的终边关于X轴它说明角与角a的正弦值对称,结合三角互为相反数,而它们的余弦值相让学生在单位圆中画出a角函数定义可得到等.这是因为,若没。的终边与与一Q角,观察两个角的位公式(二)单位圆交于点P(x,y),则角-a置关系。的终边与
4、单位圆的交点必为P(x,-y)(如图4-5-2).由正弦函数、余弦函数的定义,即可得Sina=y,cosa=x,sin(-a)=-y,cos(-a)=x,所以:sin(-a)=-sina,cos(-a)=cos公式二的获得主要借助于单位圆及正弦函数、余弦函数的定义.根据点P的坐标准确地确定点P的坐标是关键,这里充分利用了对称性质.事实上,在图1点P与点P关于X轴对称.直观的对称形象为我们准确写出P的坐标铺平了道路,体现了数形结合这一数学思想的优越性.公式(三)cosa+(2k+1)=-cosasina(2k+1)=-sinatana+(2k+1)=tana由公式(一)可以看出,角和a加上万偶数


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 诱导公式一 正弦余弦和正切的诱导公式 教学设计 诱导 公式 正弦 余弦 正切 教学 设计
 第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
第一文库网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 调和油系列产品项目可行性研究报告.doc
调和油系列产品项目可行性研究报告.doc

