专题15 圆锥曲线的中点弦问题（原卷版）.docx

《专题15 圆锥曲线的中点弦问题（原卷版）.docx》由会员分享，可在线阅读，更多相关《专题15 圆锥曲线的中点弦问题（原卷版）.docx（9页珍藏版）》请在第一文库网上搜索。

1、专题15圆锥曲线的中点弦问题一、结论221在椭圆C:9+4=1（60）中：（特别提醒此题结论适用X型椭圆）如图所示,若直线V=履0）与椭圆。交于A,B两点,过A,B两点作椭圆的切h2线有U设其斜率为:，则左滥二-勺.如图所示,若直线y=AxO）与椭圆。交于A,B两点,尸为椭圆上异于A,B的A2点,若直线PA,PB的斜率存在,且分别为ki,k2,则k1k2=-（3）如图所示,若直线y=Ax+b（左0,机0）与椭圆。交于A,5两点，尸为弦AB的中A2点,设直线PO的斜率为配则Z=-勺.图222 .在双曲线C：鼻4=1（。力0）中,类比上述结论有：（特别提醒此题结论适用X型3 双曲线）4 .在抛物线

2、C：y2=2px（p0）中类比1（3）的结论有=%（为。）.特别提醒：圆锥曲线的中点弦问题常用点差法，但是注意使用点差法后要检验答案是否符合题意；另外也可以通过联立+韦达定理求解.二、典型例题221.（2023内蒙古海拉尔第二中学高三期末（文）设椭圆的方程为。+=1,斜率为左24的直线不经过原点。而且与椭圆相交于A,B两点，M为线段AB的中点，下列结论正确的是（）A.直线AB与（W垂直;B.若直线方程为y=2x+2,贝”AB=g.C.若直线方程为y=x+1,则点坐标为，|D.若点坐标为（1,1）,则直线方程为2x+y-3=0；【答案】D【详解】2222不妨设AB坐标为（,%）,（%,%），则为

3、+=1,2+比=1,两式作差可得:24247T=-设MG。，），则9左7.vI,V-V,A对A：kABxkOM=kx=-2,故直线A氏OM不垂直，贝IJA错误；对B：若直线方程为y=2x+2,联立椭圆方程2/+V=4,42可得：61+84=0,解得玉=0,%2=-，故弘=2,%=-，贝NABI=JT+/=警,故B错误；对C：若直线方程为y+1故可得&x1=-2,即%=-2%,又为=%+1,解得%=1%=（，即加,；彳）故C错误；此题对C另解，直接利用二级结论，由于本题椭圆方程为=+!=1,是y型椭圆，所以：24V=-=-=-2,故可得生又1=2,即=2/，又%=%+1,b2Xo解得/=-1%=

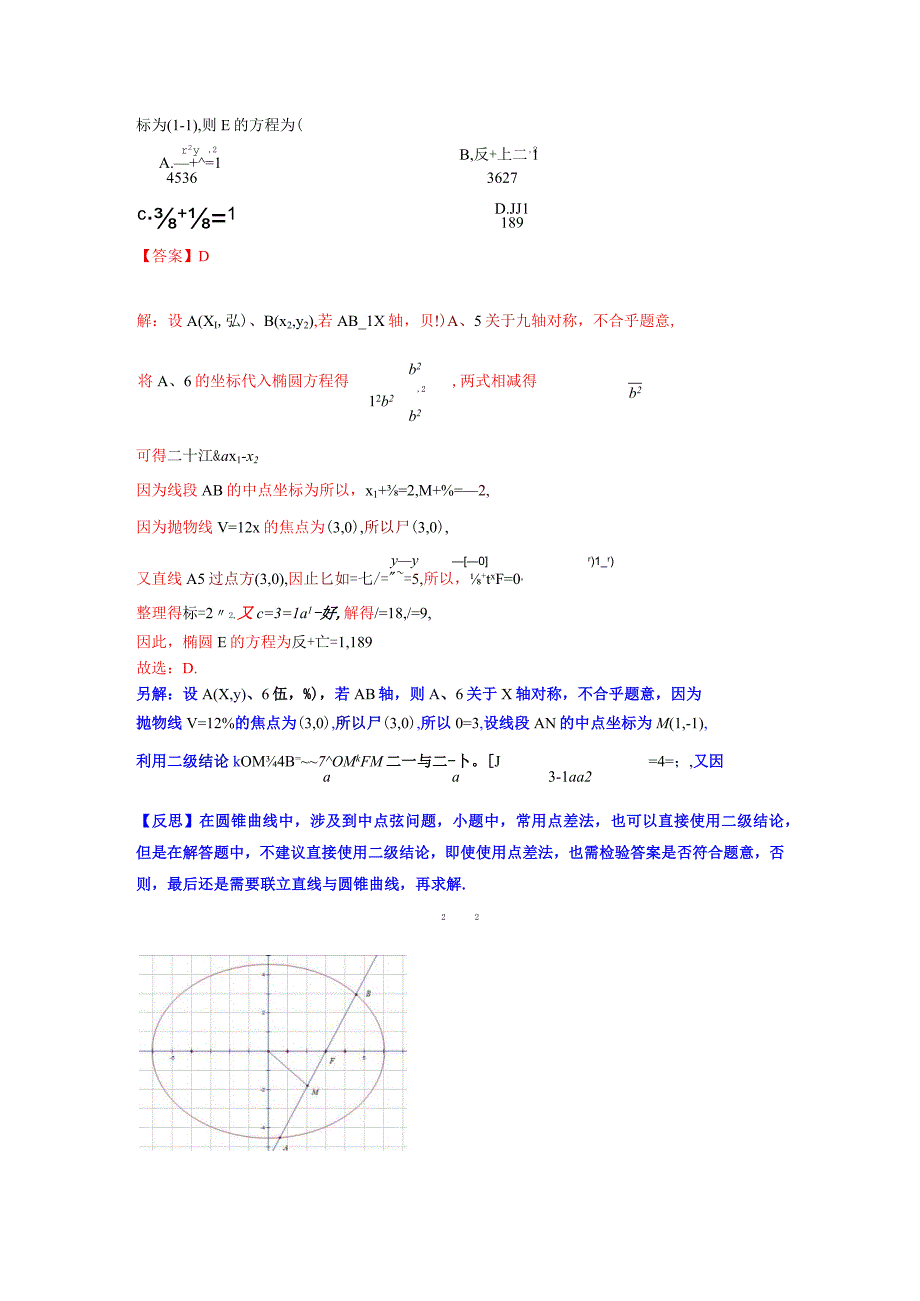
4、,即故C错误；对D：若点”坐标为（1,1）,则卜左=-2,则的1-2,又AB过点（U）,则直线AB的方程为-1=-2（x-1）,BP2%+y-3=0,故D正确.故选：D.【反思】本题考察椭圆中弦长的求解，以及中点弦问题的处理方法；解决问题的关键是利用点差法，再使用二级结论时，注意先判断椭圆是X型还是y型，再利用结论求解.222. （2023安徽淮北师范大学附属实验中学高二期中）已知椭圆石：r+%=1（。人0）的右焦点厂与抛物线丁=12%的焦点重合，过点尸的直线交E于A、6两点，若AN的中点坐标为(1-1),则E的方程为(,2r2yA.+=14536B,反+上二1,23627c+=1D.JJ11

5、89【答案】D解：设A(XI,弘)、B(x2,y2),若AB_1X轴，贝!)A、5关于九轴对称，不合乎题意,将A、6的坐标代入椭圆方程得b2,2,两式相减得12b2b2b2可得二十江&ax1-x2因为线段AB的中点坐标为所以，x1+=2,M+%=2,因为抛物线V=12x的焦点为(3,0),所以尸(3,0),yy0r)1_r)又直线A5过点方(3,0),因止匕如=七/=5,所以，+txF=0,整理得标=22,又c=3=1a1-好,解得/=18,/=9,因此，椭圆E的方程为反+亡=1,189故选：D.另解：设A(X,y)、6伍，%)，若AB轴，则A、6关于X轴对称，不合乎题意，因为抛物线V=12%

6、的焦点为(3,0),所以尸(3,0),所以0=3,设线段AN的中点坐标为M(1,-1),利用二级结论kOM4B=7OMkFM二一与二-卜。J=4=；,又因aa3-1aa2【反思】在圆锥曲线中，涉及到中点弦问题，小题中，常用点差法，也可以直接使用二级结论，但是在解答题中，不建议直接使用二级结论，即使使用点差法，也需检验答案是否符合题意，否则，最后还是需要联立直线与圆锥曲线，再求解.223. （2023湖北高二阶段练习）已知斜率为1的直线与双曲线C:2二1（0/0）相交于A、6两点，。为坐标原点，AB的中点为尸，若直线OP的斜率为2,则双曲线。的离心率为（）A.3B.2C.5D.3【答案】A【详解

7、】4-4=272设A（X，%）、B（X2，%）、P（,%）,贝22,三_&=112b2两式相减得二W=二或，所以&=工2.abxi-x2a+y2gx1+x2=2x0,j1+j2=2j0,所以2二冬.血.x1-x2ay0因为kAB=一=1,%二儿二2,所以=1,故。=2,-2a2a2故选：A.另解：直接利用双曲线中的二级结论，刀22kgk=-n2X1=-=Z?2=2a1=C22=2a2=e2=3=e=y3.aa【反思】注意使用二级结论的公式，一定要先判断，第一判断曲线是椭圆，还是双曲线，还是抛物线，第二判断圆锥曲线是X型，还是y型，第三，根据判断选择合适的二级结论，代入计算.4.（四川省蓉城名校

8、联盟2023-2023学年高二上学期期末联考理科数学试题）已知抛物线f=2py（p0）,过其焦点且斜率为1的直线交抛物线于A,B两点，若线段AB的中点的横坐标为3,则该抛物线的准线方程为（）33A.=3B.y=C.X=-3D.X=22【答案】B【详解】解：根据题意，设A(M,%),5(%2，%)，所以片=2夕%，x；=2p%，所以，得：(X%)(%+工2)=2P(X%)，即左AB二X%=：二2,、，、X1-X2/P因为直线AB的斜率为1线段AB的中点的横坐标为3,所以Kb=A=亨=2=1,即P=3,x1-X22pp所以抛物线犬=6,，准线方程为=-.故选：B【反思】在抛物线C：产=2内(夕0)

9、中类比1(3)的结论有=(WO),注意到%本题的抛物线方程是f=2py(p0),此时中点弦二级结论有Z=E,直接代入P31=n=3,小题都可以用二级结论直接求解，但是注意先判断适用条件.P5.(2023江西南昌市新建区第一中学高二期末(理)已知斜率为左(左。)的直线/与抛物线C：V=4x交于AB两点，。为坐标原点，Af是线段AN的中点，尸是。的焦点，AOFM的面积等于3,贝廉=()11126A.-B.-C.-D.4323【答案】B【详解】由抛物线Uy2=4x知：焦点方(1O)设A(,%),5(%2,%),M(,%),f2%=M+X7因为V是线段A5的中点，所以0122为=%+%将弘2=4再和%

10、?=4两式相减可得：2-y22=4(-)，7y1-%2即=J1)2=一-%,kQ:.J00SkoFM=gx1x%=3,yo=6,7221k=Z_一一九一6一3故选：B另解：因为抛物线方程Uy2=4x,设A5的中点M(%,%),由中点弦二级结论，可知:p2Z=1(%)代入：k=一,另焦点尸(i,o),因为面积鼠“M=3,可知九为1 7271SAOFM=x1Xyo=3,.=6,再代入Z=-=【反思】中点弦，最典型的方法就是点差法，在判断条件满足二级结论时，可直接使用二级结论.6.(2023湖北武汉市第十五中学高二期末)已知椭圆。的中心在原点，焦点在X轴上，长轴长为4,且点(1,白)在椭圆上.经过点

11、M(1g)作一直线乙交椭圆于A3两点，若点为线段AB的中点，求直线乙的斜率；【答案】-g;.22解：由题设椭圆的方程为土+多=1,4b因为椭圆经过点(1,白)，所以:+-=,.)=,所以椭圆的方程为:W=1所以(X1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,由题得X%2,所以(国+九2)+4(%+%)$%=0,X1-X2所以2+4XIX上二匹二0,所以2+4X1XAW=。,.七二1，七一92所以直线4的斜率为-1,经检验I1的斜率等于-1复合题意.【反思】在圆锥曲线中，涉及中点弦常用点差法，注意使用点差法，最后需检验，特别是多个答案时，更应该检验，最后保留下符合题意的答案。另

12、外中点弦问题也常联立直线和圆锥曲线，通过韦达定理来求解.特别提醒，解答题中，不能直接使用中点弦的二级结论,解答题中要先证后用.8.（2023甘肃民勤县第一中学高二阶段练习（理）若直线y=丘-2与抛物线y2=8交于A、B两点，且AB中点的横坐标为2,求此直线方程.【答案】y=2x-2【详解】y=kx-2解法一：设4%b）、B（x2,y2）,则由：H2得：y=8xV-（4+8）x+4=0.直线与抛物线相交，.0且A0,则左1且左0.4_.,r,_1、rX1+X74左+8C,AB中点横坐标为：-一二2/=2,解得：k=2或k=-1（舍去）.故所求直线方程为：y=2x-2.解法二:设4七,%）、3（,

13、为），则有其2=8%2=8.y1yo8两式作差得：（%-%）（%+%）=8（%-），即二一一.-+J2/x1+X2=4,/.y1+y2=fcr1-2+fcr2-2=左（X1+x2）-4=4-4,Q：.k=故左=2或左=一1.4k-4CyJj2联立得女2/（4左+8）x+4=0,y=8X由左0且A=（4k+8）216左2=64（左+1）0得左1且左0,故舍去左二1,则所求直线方程为：y=2x-2.【反思】在本题中，涉及中点弦问题，提供了点差法，联立直线与圆锥曲线的方法，注意在解法二中，使用点差法，但是最后的答案出现了左=2或左=-1这两个答案，此时必需要检验.三、针对训练举一反三一、单选题1（2

14、023江苏津阳高二期末）将V+/=4上各点的纵坐标不变，横坐标变为原来的2倍，得到曲线G若直线/与曲线C交于A,B两点，且AB中点坐标为M（11）,那么直线/的方程为（）A.x+2y-2=OB.x-2y=0C.2x-y-3=QD.2x+y+2=0rn2.（2023湖南长沙高三阶段练习）已知机，n,s,彳为正数，m+=4,-+-=9,其中Stm,是常数，且s+%的最小值是，点M（）是曲线二十=1的一条弦AB的中点，贝U982弦AB所在直线方程为（）A.-4y+6=0B.4-y6=0C.4x+y-10=0D.x+4y-10=0223. （2023江苏盐城高二期末）椭圆/+5=1中以点V（2,1）为中点的弦所在直线斜率为（）